Time to bring back the question that I left with a few entries ago. What about the black keys on the piano? How do they fit in? Why do we need to have them at all?
Let's start with a C major scale once again. This time, I'm presenting it both ascending and descending, so you can hear it better.
Note that it's all white keys. C D E F G A B C. C B A G F E D C. If you see a white note, play it. Easy.
Well, what about a different scale? One that starts and ends on a different note? Suppose I'm a soprano. That middle C is at the bottom of my range, it's not a note that sounds good for me. But if I started at F, and went up to F and came back down, those are notes I'm more comfortable singing. So what about an F major scale? What does an F major scale look like?
Naively, I might think that all I have to do is use the same notes I used before to make the C major scale, but just start on F and end on F.
F G A B C D E F. F E D C B A G F.
But if I do that, this is what it sounds like:
It doesn't sound right. The fourth note in the scale is off. But why?
The answer to that question goes back to Pythagoras. If you recall from Donald Duck's trip to Mathemagic Land, the notes in a scale are all related to each other by ratios of frequency. The ratio between C and F, for example, is 4/3: for every 3 times a C string vibrates, the F string vibrates 4 times. If B were the fourth note in an F major scale, its frequency would have to be (4/3) * (4/3) that of C, or 16/9.
But that's not the way it works out. There is no note in the C major scale whose frequency is 16/9 that of C. A is too low; B is too high. So the fourth note in the F major scale has to be some different note, a note that's in between A and B. It's like we took a B, and bent its pitch down just enough to make it fit and sound right in an F major scale. We call this note...
B flat!!!
And this is how B flat is written in staff notation. The note takes the same position on the staff as a B does - it's on the third line, the one right in the middle. But see that little ♭ sign in front of the B note? That ♭ sign is a flat. Flat means that you take the note and lower its pitch just a little bit.
So now that we have our B flat, we can fix our F scale. Now it sounds like this:
Voilà!
Next, let's consider a G scale. Starting with G:
G A B C D E F G. G F E D C B A G.
This time, it's not the fourth note that's off. It's the seventh. That F doesn't sound right, it's too low for the scale. So we raise it up a bit:
Our new note is F sharp. Sharps are denoted by a # sign in front of the note. They're the opposite of flats - a sharp sign in front of a note raises the pitch just a little bit.
What about plain white notes? Don't they get a symbol too? Of course they do! You might recognize this tune from Gershwin, which makes use of the symbol we need.
Notice how the two Bs are flatted in measures 5 and 6, but each one of them is followed by another B with a funny looking sign in front of it. That sign is called a natural sign. A natural sign means that the note is neither sharp nor flat. Normally it's used only to cancel out a sharp or flat sign that came earlier - you don't have to write a natural sign for every note.
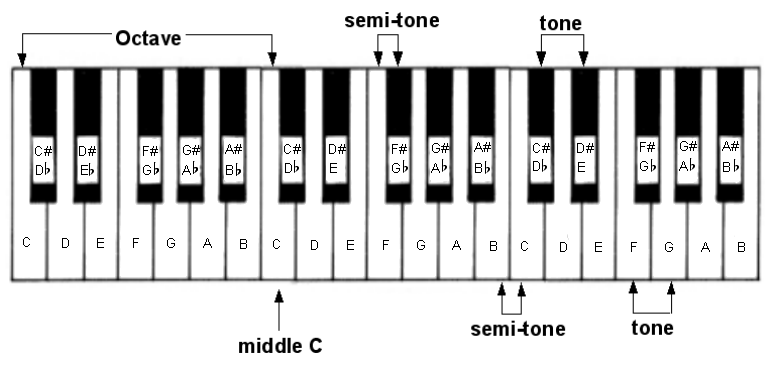
So now our piano keyboard is complete. We now have name for those five black keys on the keyboard:
The note in between C and D is C sharp, or D flat.
The note in between D and E is D sharp, or E flat.
The note in between F and G is F sharp, or G flat.
The note in between G and A is G sharp, or A flat.
The note in between A and B is A sharp, or B flat.
On the diagram above, you can see an octave labeled. There's also two other terms there that are very useful to know: semitone, and tone. A semitone is the interval between one note and its nearest neighbor, up or down. The notes F and F# differ by a semitone. So do the notes B and C, because they're right next to each other. When you put two semitones together, you get a tone, or a whole tone. C# and D# are a whole tone apart: from C# to D is a semitone, from D to D# is another semitone, and two semitones put together make a whole tone. From F to G is also a whole tone. F to F#, F# to G - each one of those steps is a semitone.
(You'll often hear the words half step and whole step used, instead of semitone and whole tone. They mean exactly the same thing.)
Next time, we'll use semitones and whole tones (or half steps and whole steps) to show how major and minor scales are built.
No comments:
Post a Comment